
Wir Menschen haben an jeder Hand 5 Finger, insgesamt logischerweise also 10 Stück. Es ist daher nur natürlich, dass wir das dezimale Zahlensystem haben, wir also unsere Zahlen in Zehnerschritten unterteilen.
Die Na’vi haben allerdings insgesamt nur 8 Finger, 4 an jeder Hand (ja, Daumen werden in dem Fall mitgezählt, hrh).
Sie zählen also nicht bis 10 bzw. in Zehnerschritten so wie wir, sondern in Achterschritten - sie nutzen das oktale Zahlensystem.
Aber um dieses vielleicht verwirrend erscheinende oktale System zu verstehen, müssen wir erst einmal verstehen, wie unser eigenes dezimales System aufgebaut ist und funktioniert. Um dies zu erklären behelfe ich mich mal Tekres Erklärung, die sie mir und somit euch freundlicherweise für diese Lektion zur Verfügung gestellt hat (irayo nìtxan nìmun!) 
„Um zu verstehen, wie das Na’vi-System funktioniert, sollte man vielleicht erst mal allgemein wissen, wie ein Stellenwertsystem funktioniert.
Ein Stellenwertsystem bedeutet einfach, dass eine Ziffer in einer Zahl je nachdem, an welcher Stelle sie steht, unterschiedlich viel Wert hat. Beispiel aus unserem dezimalen System:
757 = 7x100 + 5x10 + 7x1
(7x10^2 + 5x10^1 + 7x10^0)
Die letzte Stelle ist also 10^0 (1) wert, mal die Zahl, die dort steht. Die nächste Stelle ist 10^1 (10) wert, die nächste 10^2 (100) und so weiter. Wir benutzen also das 10er System. Das System kann man aber auch mit jeder anderen Zahl umsetzten. Beispiel: das oktale System. Dabei setzt man überall anstatt der 10 die 8 ein. Beispiel:
757 (oktal) = 7x64 + 5x8 + 7x1
(7x8^2 + 5x8^1 + 7x8^0)
Wenn man das ausrechnet (indem man das ausrechnet bekommt man wieder eine dezimale, also für uns normale Zahl) kommt man auf 495 – also was ganz anderes. 757 (oktal) und 495 (dezimal) sind also gleich viel wert – es ist die gleiche Zahl in verschiedenen Zahlensystemen. Normalerweise sind Zahlen, bei denen nicht genauer angegeben ist, aus welchem System sie stammen, unsere normalen dezimalen Zahlen, ist eine Zahl im oktalen System notiert steht normalerweise noch eine tiefgestellte 8 hinten dran (8) oder einfach, wie ich es gerade mache, „(oktal)”.” - Tekre
Klar? Verwirrt? Lasst uns mal kurz einen Blick auf die oktalen Zahlen blicken, dann wird vielleicht klarer was gemeint ist - zumindest hoffe ich das  Schaut euch die Zahlen („Kardinalszahlen”) in Ruhe an, auch, wie sie logisch bzw. rechnerisch zusammengesetzt sind.
Schaut euch die Zahlen („Kardinalszahlen”) in Ruhe an, auch, wie sie logisch bzw. rechnerisch zusammengesetzt sind.
Kardinalszahlen
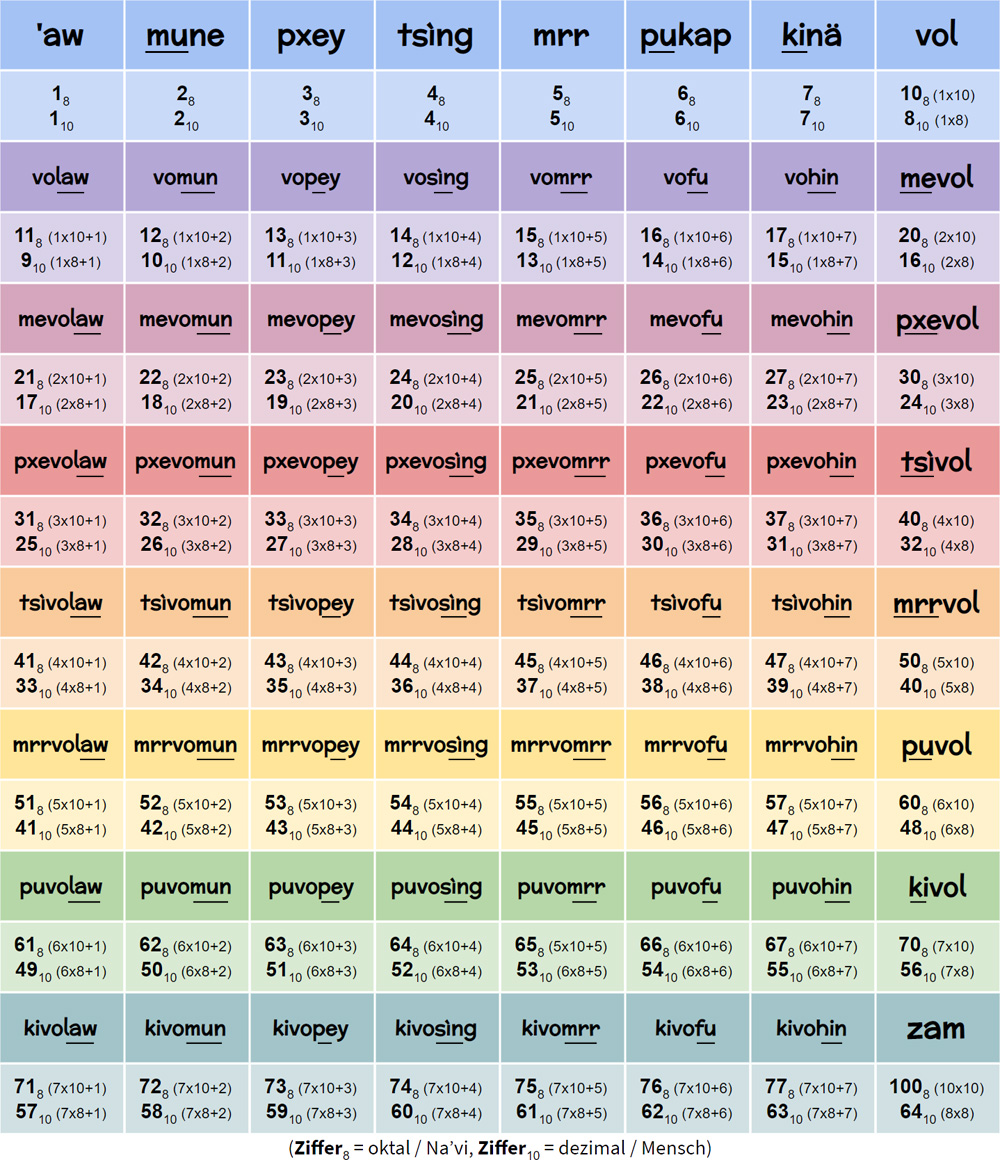
Wie man sehen kann, werden lenierte (und z.T. verkürzte) Versionen der Zahlen 1 - 7 (-aw, -mun, -pey, -sìng, -mrr, -fu, -hin) an vol angehängt, um neue Zahlen zu bilden (ähnliches Phänomen wie bei den Mehrzahlpräfixen). Ab 1610 (2 x 8) wird das Präfix für „zwei” (me+) vor vol gesetzt; dasselbe passiert mit pxe-; ab tsì- werden aber wieder verkürzte Zahlen als Präfixe verwendet.
Klar sollte werden: was für uns 10010 ist, ist für die Na’vi 6410. Bzw. was für uns 6410 ist, ist für die Na’vi 1008.
Wie zählt man aber über 6410 / 1008 hinaus?
Nun, ab da geht’s dann einfach mit zam weiter! Zamaw (8² bzw. 64 + 1), (ab jetzt dann ohne m von zam, da die nächsten Silben mit Konsonanten beginnen) zamun, zapey, usw. … bis man bei 72 ankommt, dann hört es nicht mehr bei 7 auf, sondern geht bis 8 weiter, also zavol. Ab da wird dann wie gewohnt weitergemacht; zavolaw, zavomun, …bis 80, zamevol. Ab da dann zamevolaw, zamevomun, … und so weiter.
Etwas übersichtlicher (erinnert euch, ob nun dezimal oder oktal, es sind nur verschiedene Darstellungsweisen der selben Zahl, je nach Zahlsystem; ähnlich wie unterschiedliche Angaben in °C und °F dennoch die selbe Temperatur meinen):
| Oktal8 | Dezimal10 | Oktal8 | Dezimal10 | Oktal8 | Dezimal10 |
| zam = 100 zamaw = 101 zamun = 102 zapey = 103 zasìng = 104 zamrr = 105 zafu = 106 zahin = 107 zavol = 110 zavolaw = 111 zavomun = 112 zavopey = 113 zavosìng = 114 zavomrr = 115 zavofu = 116 zavohin = 117 |
64 = 82 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 |
zamevol = 120 zamevolaw = 121 zamevomun = 122 zamevopey = 123 zamevosìng = 124 zamevomrr = 125 zamevofu = 126 zamevohin = 127 zapxevol = 130 zapxevolaw = 131 zapxevomun = 132 zapxevopey = 133 zapxevosìng = 134 zapxevomrr = 135 zapxevofu = 136 zapxevohin = 137 |
80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 |
zatsìvol = 140 zatsìvolaw = 141 zatsìvomun = 142 zatsìvopey = 143 zatsìvosìng = 144 zatsìvomrr = 145 zatsìvofu = 146 zatsìvohin = 147 zamrrvol = 150 zamrrvolaw = 151 zamrrvomun = 152 zamrrvopey = 153 … vozam = 1000 … zazam = 10000 |
96 97 98 99 100 101 102 103 104 105 106 107 … 512 = 83 … 4096 = 84 |
Ich war mal so frei, nicht nur Tekre’s großartige Erklärung, sondern auch die folgende Tabelle von Tìtstewan zu mopsen 
| Zahl10 | Zahl8 | Na’vi | Grundzahl | Restform |
| 0 | 0 | kew | ||
| 1 | 1 | ‘aw | -aw | |
| 2 | 2 | mune | me- | -mun |
| 3 | 3 | pxey | pxe- | -pey |
| 4 | 4 | tsìng | tsì- | -sìng |
| 5 | 5 | mrr | mrr- | -mrr |
| 6 | 6 | pukap | pu- | -fu |
| 7 | 7 | kinä | ki- | -hin |
| 8 | 10 | vol | vo- | |
| 64 (82) | 100 | zam | za- | |
| 512 (83) | 1000 | vozam | voza- | |
| 4096 (84) | 10000 | zazam | zaza- |
Das ist rein theoretisch alles, was ihr zum Bilden selbst der höchsten Zahlen braucht.
Wenn euch das nicht reicht, ihr vielleicht sogar manuell von dezimal zu oktal umrechnen lernen wollt etc., lest in dieser Lektion weiter und / oder werft einen zusätzlichen Blick in die weiterführende Liste bzw. Erklärung der Zahlen von Tìtstewan: http://files.learnnavi.org/docs/Das_Navi_Zahlen-System_V2-6.pdf
Kew ist übrigens eine abgewandelte Form von ke’u (nichts / „keine Sache”).
Weiter geht’s mit Tekres Worten:
„Die Na’vi sagen jetzt alles im oktalen System. Würde ein Na’vi also schreiben lernen und 757 aufschreiben, würde er damit die oktale Version dieser Zahl meinen: Statt 7x100 + 5x10 + 7x1 würde er also 7x64 + 5x8 + 7x1 meinen, also ausgerechnet würde er aus unserer Sicht eigentlich 495 meinen.
Auch der sprachliche Aufbau richtet sich danach: statt siebenmal-hundert (7x100 = 700 (dezimal)) sagen sie also siebenmal-vierundsechzig (7x64 = 700 (oktal) oder auch, „richtig” ausgerechnet, 448 (dezimal)).
Oder, um unsere Beispielzahl komplett zu nehmen: Wenn wir die 757 sehen sagen wir siebenmal-hundert_fünfmal-zehn_sieben, oder kurz: siebenhundertsiebenundfünfzig. Ein Na’vi allerdings sagt siebenmal-vierundsechzig_fünfmal-acht_sieben. Oder, übersetzt, kiza-mrrvo-hin. Und wenn man wortwörtlich nimmt, was die Na’vi sagen, merkt man ja schon, dass da eine völlig andere Zahl rauskommt, nämlich unsere 495.
Am besten kann man sich das wirklich mit Beispielen verdeutlichen. Nehmen wir einfach mal zam, von dem es immer heißt, es wäre 100. Das ist sowohl richtig als auch falsch, denn es ist nur im oktalen System die 100. Wenn man es in unser dezimales System umrechnet, sieht das so aus:
100 (oktal) = 1x64 + 0x8 + 0x1 = 64 (dezimal)
Wenn ich also sage, ich habe zama ioang in meinem Zoo, habe ich keine 100 Tiere, sondern eigentlich nur 64 – obwohl zam im oktalen System geschrieben 100 ist. Wie gesagt, hier ist es sehr wichtig zu unterscheiden: Steht die Zahl im oktalen oder im dezimalen System?
(Diese Verwirrung ist übrigens ein Grund, weshalb ich mich immer aufrege, wenn Leute sagen, dass zam hundert bedeutet, aber nicht dazuschreiben in welchem System – kein Wunder, dass so viele Probleme damit haben. Ich bin dafür, dass sämtliche neuen User erst einmal eine Einführung in Zahlensysteme bekommen bevor man sie auf die verwirrenden Chats loslässt  )
)
Doch was mache ich jetzt, wenn ich sagen möchte, dass ich 100 (dezimal) Tiere habe? Dazu muss man die 100 (dezimal) ist eine oktale Zahl umwandeln. Dazu gibt es zwei Möglichkeiten. Erste Möglichkeit:
Ich schaue zuerst, wie oft passt die 64 (dezimal) in die 100 (dezimal). Das ist genau ein Mal, also fängt meine Zahl mit zam- an, oder, in Ziffern geschrieben, mit 1. Und da die 64er im oktalen System an der dritten Stelle von rechts stehen ergänzen wir das noch: 100 (oktal).
Dann bleiben noch 36 übrig. Wir schauen, wie oft passt die 8 in die 36: vier Mal. Wir können unsere Zahl also auf zatsìvol bzw. auf 140 (oktal) ergänzen.
Jetzt bleiben nur noch 4 übrig. Die letzte Stelle beinhaltet die 1er, und die eins passt logischerweise vier Mal in die 4, also können wir unsere Zahl vervollständigen: zatsìvosìng, oder in Zahlen geschrieben: 144 (oktal). Zatsìvosìnga ioang / °144a (oktal) ioang = 100 Tiere bei uns.
Oder man kann auch meine Methode [„Division/Rechnen mit Rest” - Anm. v. Kris] anwenden und immer durch 8 Teilen:
100/8 = 12 Rest 4
12/8 = 1 Rest 4
1/8 = 0 Rest 1
→ aus der 100 (dezimal) wird die 144 (oktal).
Wichtig: Das Ergebnis ist bereits die umgerechnete, oktale Zahl! Man liest sie jetzt also nicht mehr einmal-hundert_viermal-zehn_viermal-eins sondern wir lesen diese Zahl jetzt wie die Na’vi: einmal-vierundsechzig_viermal-acht_viermal-eins. Sie hat also bereits genau dieselbe Struktur wie die Sprache und kann daher 1 zu 1 übersetzt werden: za(m)-tsìvo(l)-(t)sìng. Zatsìvosìng.
Wie oben steht, kann man dieses Ergebnis auch einfach wieder in unser dezimales System umwandeln, indem wir es einfach ausrechnen:
144 (oktal) = 1x64 + 4x8 + 4x1 = 64 + 32 + 4 = 100 (dezimal)
So, keine Ahnung, ob das jetzt verständlicher war oder noch verwirrender  Wenn man sich aber mit den ganzen Zahlen nicht beschäftigen will sollte man vielleicht noch wissen, dass man bei dict-navi immer die dezimale Zahl eingibt, das wird dann automatisch in oktal umgerechnet und übersetzt. ” - Tekre
Wenn man sich aber mit den ganzen Zahlen nicht beschäftigen will sollte man vielleicht noch wissen, dass man bei dict-navi immer die dezimale Zahl eingibt, das wird dann automatisch in oktal umgerechnet und übersetzt. ” - Tekre
Nehmen wir dennoch mal nach Tekres Erklärung und Methode ein paar Zahlen und üben das Ganze.
| Beispielzahl 99. Man teilt ja, wie Tekre erwähnt hat, immer durch 8: 99 / 8 = 12, Rest 3. (12 x 8 = 96; 99 - 96 = 3) 12 / 8 = 1, Rest 4. (1 x 8 = 8; 12 - 8 = 4) 1 / 8 = 0, Rest 1. Jetzt nimmt man die Ziffern, die als Rest übrig geblieben sind, von hinten nach vorne und daraus ergibt sich dann das (oktale/„Na’vi”)Ergebnis 143. |
Beispielzahl 34. 34 / 8 = 4, Rest 2. 4 / 8 = 0, Rest 4. Ergebnis: 42. |
| Beispiel 243. 243 / 8 = 30, Rest 3. 30 / 8 = 3, Rest 6. 3 / 8 = 0, Rest 3. Ergebnis: 363. |
Beispiel 428. 428 / 8 = 53, Rest 4. 53 / 8 = 6, Rest 5. 6 / 8 = 0, Rest 6. Ergebnis: 654. |
Jetzt fehlt nur noch das Ganze auch wie ein Na’vi auszusprechen.
Wir erinnern uns, wir sprechen unsere Zahlen in Zehnerschritten aus, 10000, 1000, 100, 10, 1;
zweihundertsiebenunddreißig = zweimal-hundert_dreimal-zehn_sieben(mal-eins) = 237 (dezimal10).
Bei den Na’vi sehen die Schritte (aus dezimaler Sichtweise) jedoch so aus: 4096, 512, 64, 8, 1;
dreimal-vierundsechzig_fünfmal-acht_fünf(mal-eins) = 355 (oktal8) = pxezamrrvomrr.
Deswegen ist zweihundertsiebenunddreißig auf Na’vi pxezamrrvomrr.
Warum nochmal 4096, 512, 64, 8, 1? Erinnerung:
| Oktal8 | Dezimal10 |
| ‘aw = 1 vol = 10 zam = 100 vozam = 1000 zazam = 10000 |
1 8 64 = 82 512 = 83 4096 = 84 |
Wenden wir die Übersetzung mal auf die Beispielzahlen von gerade eben an:
| 9910 = 1438 einmal-vierundsechzig_viermal-acht_drei(mal-eins) = zatsìvopey. |
3410 = 428 viermal-acht_zwei(mal-eins) = tsìvomun. |
| Rechen- und Übersetzungsweg ohne „Rechnen mit Rest”: 64 passt in 99 einmal rein, also haben wir schon einmal 1 x 64, zam. Bis 99 fehlen uns aber noch 35 (99-64=35). In 35 passt die 8 viermal rein, (4 x 8=32), tsìvol. Bis 35 fehlen noch 3 (35-32=3), pxey. Zusammengenommen: zatsìvopey, 1438. |
Alternativmethode: 8 passt in 34 viermal rein (4x8=32), tsìvol. Fehlen noch 2 bis 34 (34-32=2), mune. Zusammen: tsìvomun, 428. |
| 24310 = 3638 dreimal-vierundsechzig_sechsmal-acht_drei(mal-eins) = pxezapuvopey. |
42810 = 6548 sechsmal-vierundsechzig_fünfmal-acht_vier(mal-eins) = puzamrrvosìng. |
| Alternative: In 243 passt 64 dreimal rein (3x64=192), pxezam. Fehlen noch 51 (243-192=51). Da passt 8 sechsmal rein (6x8=48), puvol. Bis 51 fehlen aber noch 3, pxey. Zusammen: pxezapuvopey, 3638. |
Alternative: In 428 passt 64 sechsmal rein (6x64=384), puzam. Fehlen noch 44, da passt 8 fünfmal rein (5x8=40), mrrvol. Fehlen noch 4, tsìng. Zusammen: puzamrrvosìng, 6548. |
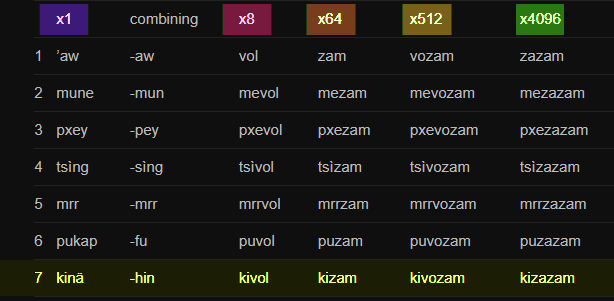
Also spätestens da hatte sogar ich Matheverweigerer das Ganze gerallt - ich hab mich sogar dann daran getraut, noch höhere Zahlen umzurechnen. Also, wie schaut es aber mit noch höheren Zahlen aus? Und welche ist die höchstmögliche Zahl, die man noch umrechnen kann? Tja, das wäre die 32767 (dezimal10) bzw. 77777 (oktal8). Warum ist sie die höchstmögliche Zahl? Deswegen:
 Quelle: https://learnnavi.org/navi-numbers/
Quelle: https://learnnavi.org/navi-numbers/
Wir haben nur diese Zahlwörter zu unserer Verfügung, um daraus entsprechendes basteln zu können. Die höchstmögliche Kombination daraus wäre also kizazakivozakizakivohin = 777778 = 3276710. Um höhere Zahlen als diese bilden zu können, benötigten wir neue Zahlwörter (z.B. für 100.0008 oder 1.000.0008) - und die haben wir nicht und werden wir vielleicht (hoffentlich?) auch nie bekommen. ^^
Ich rechne euch nochmal eine Zahl um, am Rest könnt ihr euch gerne selbst frei Schnauze oder unten in der Übung versuchen  Hmm… nehmen wir einfach mal die 753110:
Hmm… nehmen wir einfach mal die 753110:
| Division mit Rest (Tekres Favorit):
7531/8 = 941 Rest 3 |
Alternativmethode (mein Favorit):
4096 passt in 7531 1x rein = zazam. (1x4096=4096) |
Solch hohe Zahlen werdet ihr aber im Alltagsgebrauch auf Na’vi wahrscheinlich so gut wie nie verwenden. Daher reicht es eigentlich vollkommen aus bis 16 oder höchstens 24 zählen zu können, aber wir sind ja hier um möglichst viel zu lernen, nech… 
Rechnen wir nochmal etwas von oktal zu dezimal um:
Nehmen wir mal die Beispielzahl mezazapxevozatsìzamevol. Da sie auf Na’vi geschrieben ist, gehe ich davon aus, dass es sich hierbei um die oktale Zahl handelt. Dröseln wir sie mal auf:
mezazapxevozatsìzamevol = 2x10000 + 3x1000 + 4x100 + 2x10 + 0x1 = 23420.
Das ist ja aber die oktale Zahl. Jetzt müssen wir, anhand der Tabelle oben, die jeweiligen Stellenwerte vom oktalen auf’s dezimale System übertragen, das heißt, 100008 wird in der Rechnung zu 409610, 10008 wird zu 51210, 1008 zu 6410 und 108 zu 810. 1 ist und bleibt in beiden Systemen ja einfach 1. Also:
2x4096 + 3x512 + 4x64 + 2x8 + 0x1 = 10000.
Rechenweg:
2 x 4096 = 8192
3 x 512 = 1536
4 x 64 = 256
2 x 8 = 16
0 x 1 = 0
8192 + 1536 + 256 + 16 + 0 = 10000.
So, das reicht jetzt aber auch… genug Mathe für heute, wenden wir uns mal wieder der Grammatik zu! (Endlich, Eywa sei Dank!)
Anwendung von Zahlen in Sätzen
Jetzt noch etwas mehr zu der Anwendungsweise von Zahlen in Sätzen. Generell werden sie wie Adjektive an Nomen gereiht, also mit Hilfe von dem bereits bekannten -a- (dies ist aber erst wirklich nötig, wenn man mit me+ und pxe+ nicht weiterkommt):
‘awa nari / nari a’aw - ein Auge (Anzahl)
menari - zwei Augen - (merkwürdig und umständlich erscheinende) Alternative: munea nari / nari amune
pxenari - drei Augen - (merkwürdig und umständlich erscheinende) Alternative: pxeya nari / nari apxey
aynari - vier oder mehr Augen - sehr vage, oder nicht? Daher…
tsìnga nari / nari atsìng - vier Augen
mrra nari / nari amrr - fünf Augen
pukapa nari / nari apukap - sechs Augen
kinäa nari / nari akinä - sieben Augen
vola nari / nari avol - acht Augen
volawa nari / nari avolaw - neun Augen
…
mevomrra nari / nari amevomrr - 21 Augen
…
zama nari / nari azam - 64 Augen
…
und so weiter.
Oeri solalew zìsìt apxevohin. Was mich betrifft sind 31 Jahre vergangen/voran geschritten. = Ich bin 31 Jahre alt.
Ordinalszahlen
Und was ist, wenn man „das erste Buch”, „der dreizehnte Krieger”, „das siebte Wort”, ” und dergleichen sagen will? Das funktioniert, indem wir die Zahlen („Ordinalszahlen”) mit einem kleinen -ve und dem -a- für Adjektive versehen:
‘awvea puk / puk a’awve
vomrrvea tsamsiyu / tsamsiyu avomrrve
kivea lì’u / lì’u akive
Euch ist vielleicht aufgefallen, dass es kive und nicht kinäve heißt. Dahinter steckt folgende Regel:
Das Suffix -ve kann nicht beliebig an jede Ausgangsform der Zahlen gehangen werden; es ist irregulär.
In manchen Fällen nutzt es die „lange” Form (ganze Zahlen), in einigen Fällen jedoch die „kurze” Form (verkürzte Zahlworte):
Kurze Form: muve, tsìve, puve, kive
Lange / normale Form: ‘awve, pxeyve, mrrve, volve
In entsprechender Reihenfolge: ‘awve, muve, pxeyve, tsìve, mrrve, puve, kive, volve.
Bei höheren Zahlen wird das Ganze entsprechend vorhersehbar:
Volawve, vomuve, vopeyve, vosìve, vomrrve, vofuve, vohive, mevolve, mevolawve, mevomuve, und so weiter.
Bei zam, zazam und vozam streicht man quasi das m und hängt -ve an: zave, zazave, vozave.
Diese Formen sind auch mit nì- produktiv. Es gibt offiziell das Wort nì’awve (erstens) aber da dieses Schema produktiv ist, kann man selbst auch nìmuve, nìpxeyve, nìtsìve, nìmrrve, nìpuve, nìkive, nìvolve, usw. bilden.
Teile und Brüche
Und dann gibt es auch noch Teile bzw. Brüche, wobei das -ve der Ordinalszahlen schlicht durch ein -pxì ersetzt wird:
mawl - Hälfte
pan - Drittel
tsìpxì - Viertel
mrrpxì - Fünftel
pupxì - Sechstel
kipxì - Siebtel
vopxì - Achtel
Diese Liste ist beliebig fortführbar, allerdings sind diese Zahlwörter Substantive, keine Adjektive.
Übung I:
Rechnet (manuell, ohne dict-navi oder Umrechner; Taschenrechner und Kopf sind erlaubt) folgende Zahlen von dezimal zu oktal um, übersetzt sie entsprechend und bildet die entsprechenden Varianten:
- 129, einhundertneunundzwanzig Tiere, das einhundertneunundzwanzigste Tier
- 67, siebenundsechzig Bücher, das siebenundsechzigste Buch
- 15, fünfzehn Steine, der fünfzehnte Stein
- 26, sechsundzwanzig Äste, der sechsundzwanzigste Ast
- 573, fünfhundertunddreiundsiebzig Jahre, das fünfhundertunddreiundsiebzigste Jahr
- 1996, eintausendneunhundertundsechsundneunzig Stühle, der eintausendneunhundertundsechsundneunzigste Stuhl
- 395, dreihundertundfünfundneunzig Besucher, der dreihundertundfünfundneunzigste Besucher
- 666, sechshundertundsechsundsechzig Musiker, der sechshundertundsechsundsechzigste Musiker ?
- 19463, neunzehntausendvierhundertundsechsunddreißig Eier, das neunzehntausendvierhundertundsechsunddreißig Ei
Übung II:
Übersetzt folgende Zahlen bzw. nutzt sie, um von der oktalen zur dezimalen Zahl zu gelangen:
- puzapey
- pxezapxevomun
- vozapxezatsìvol
- mezazapuvozatsìzavomrr
- puzazamrrvozapxezakivolaw


